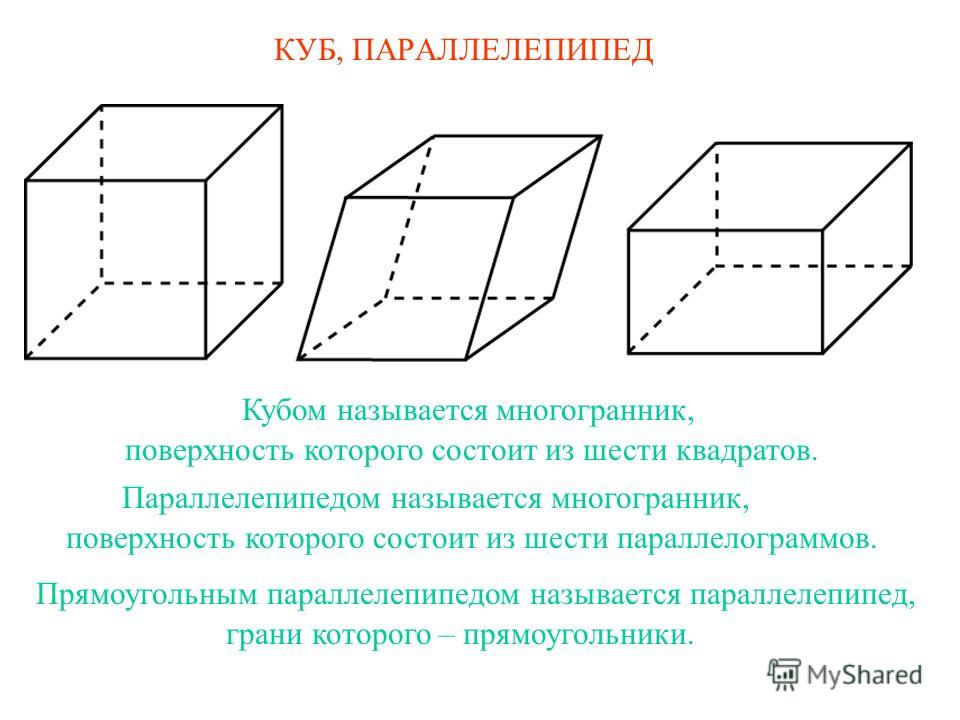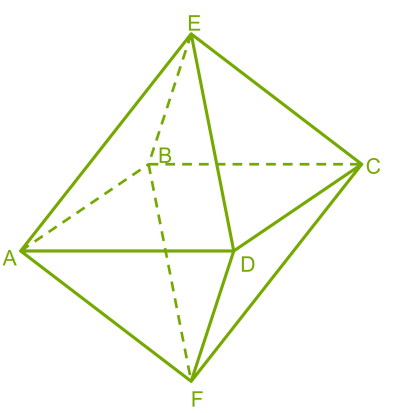
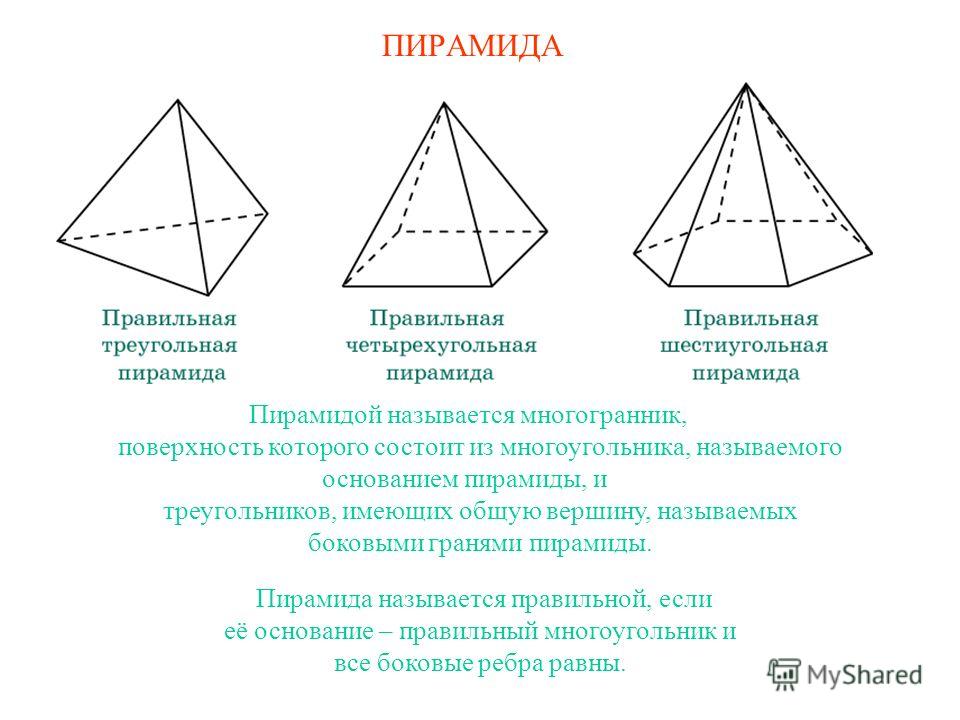
Многогранники из бумаги
В топе. Команда R. Смотреть позже.



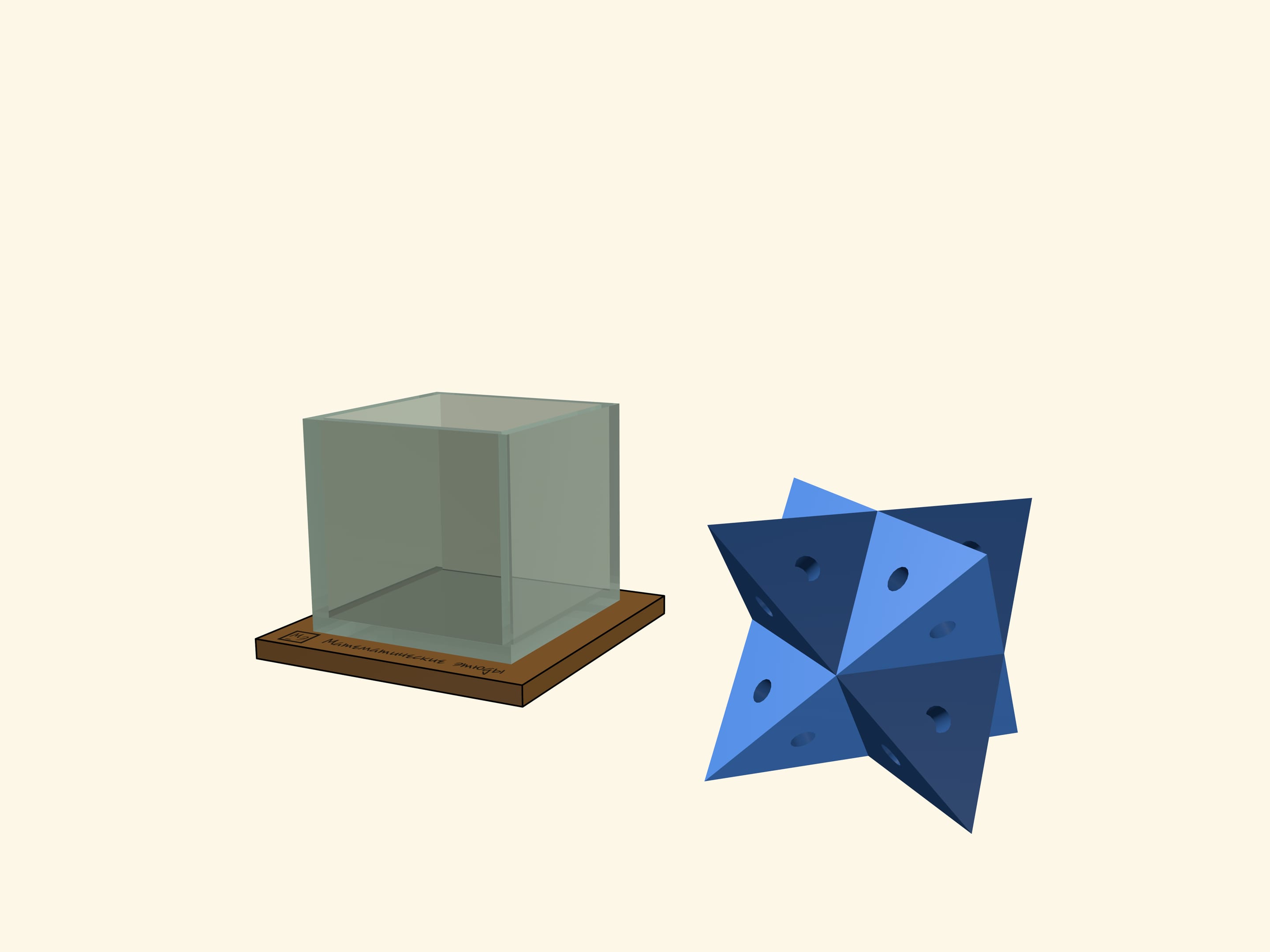

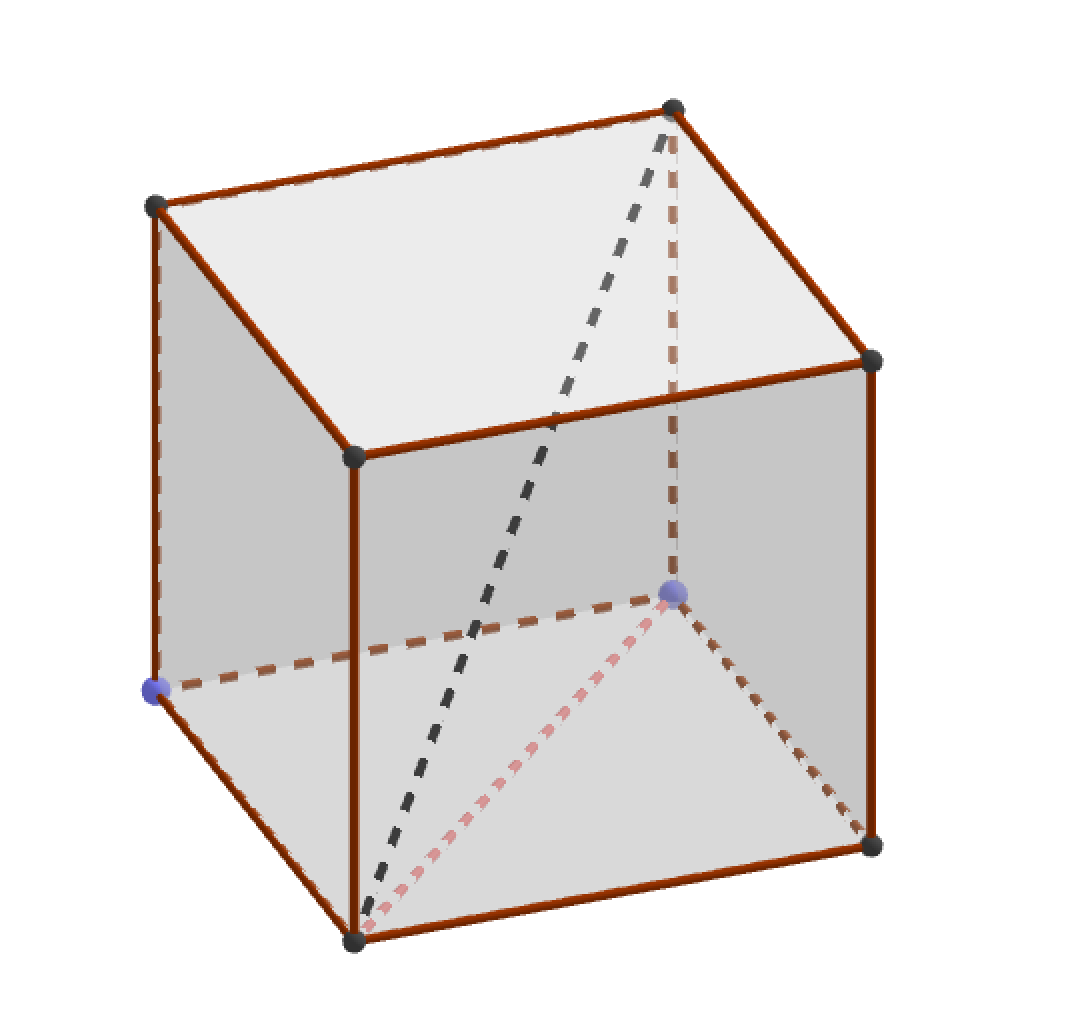
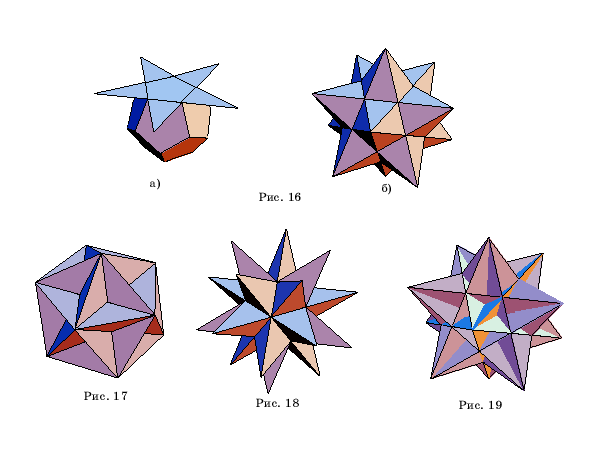

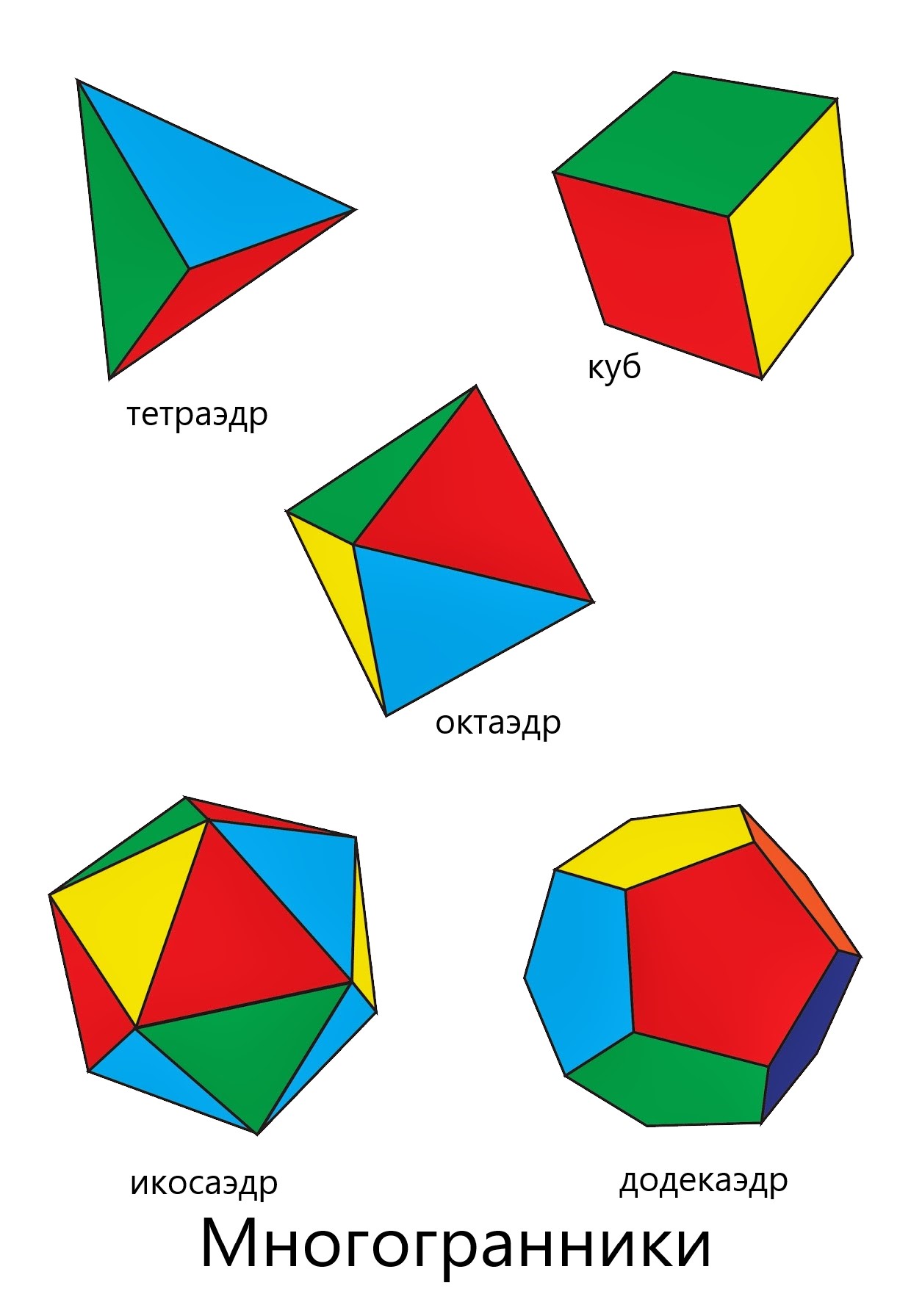
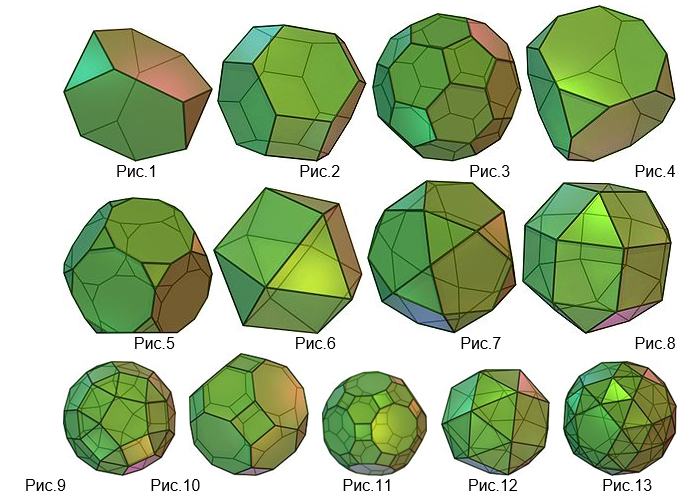


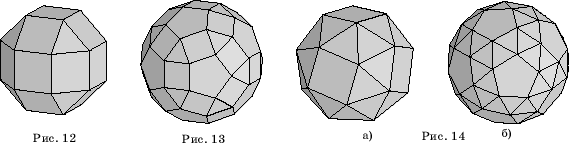
Усеченный куб принадлежит к семейству архимедовых тел , то есть полуправильных выпуклых многогранников. Усеченный куб может быть получен из куба усечением вершин. В процессе усечения грани куба превращаются в правильные восьмиугольники, а на месте удаленных вершин появляются треугольные грани. Раскраску, удовлетворяющую принципу раскраски карт можно получить, скопировав раскраску восьмиугольных граней с куба, а для треугольных граней выбрав новый цвет.
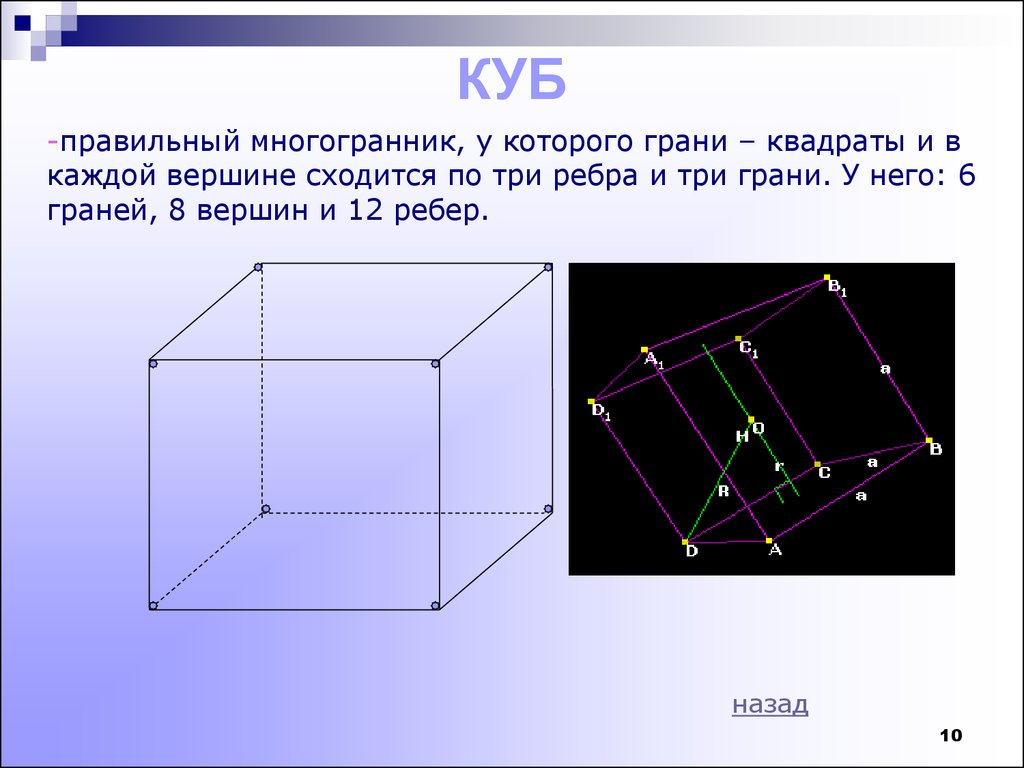
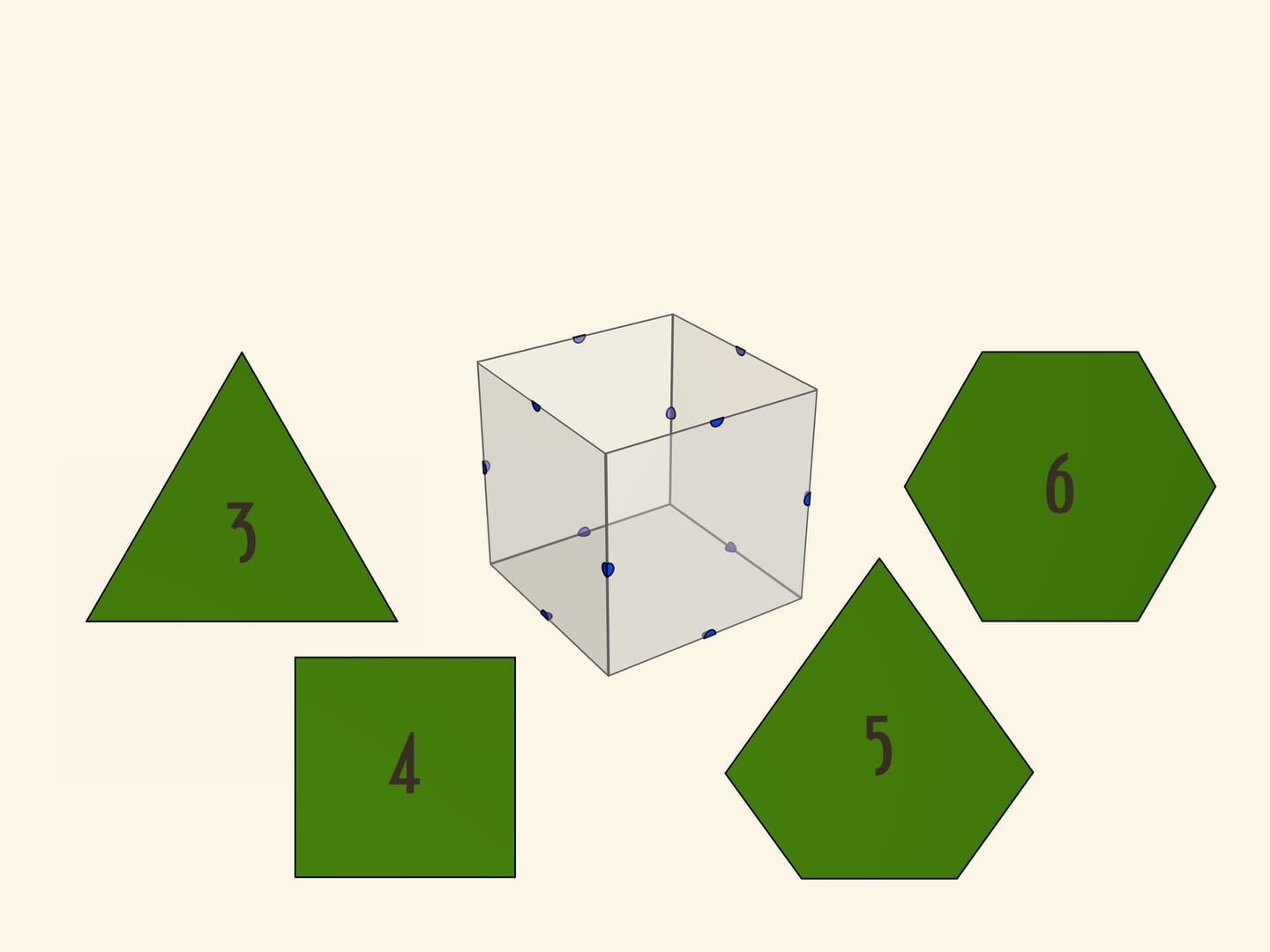
- Гексаэдр куб, четырёхугольная призма, шестигранник — многогранник, каждая грань которого представляет собой квадрат. Также является одним из пяти правильных многогранников Платоновых тел.
- Усечённый куб - полуправильный выпуклый многогранник, обладающий двумя свойствами: 1. Все грани являются правильными многоугольниками двух типов - восьмиугольник и треугольник; 2.
- Я уже давно пытаюсь понять, за счет чего при появлении в Символе дробных чисел возникает звездчатость.
- Пишите нам: e-Quadrat narod. Выпуск 1 О чём рубрика?
- Андреев, С. Этюды Модели Миниатюры iMath Лекции.
- Составлен из 22 граней: 12 правильных треугольников , 5 квадратов и 5 правильных восьмиугольников.

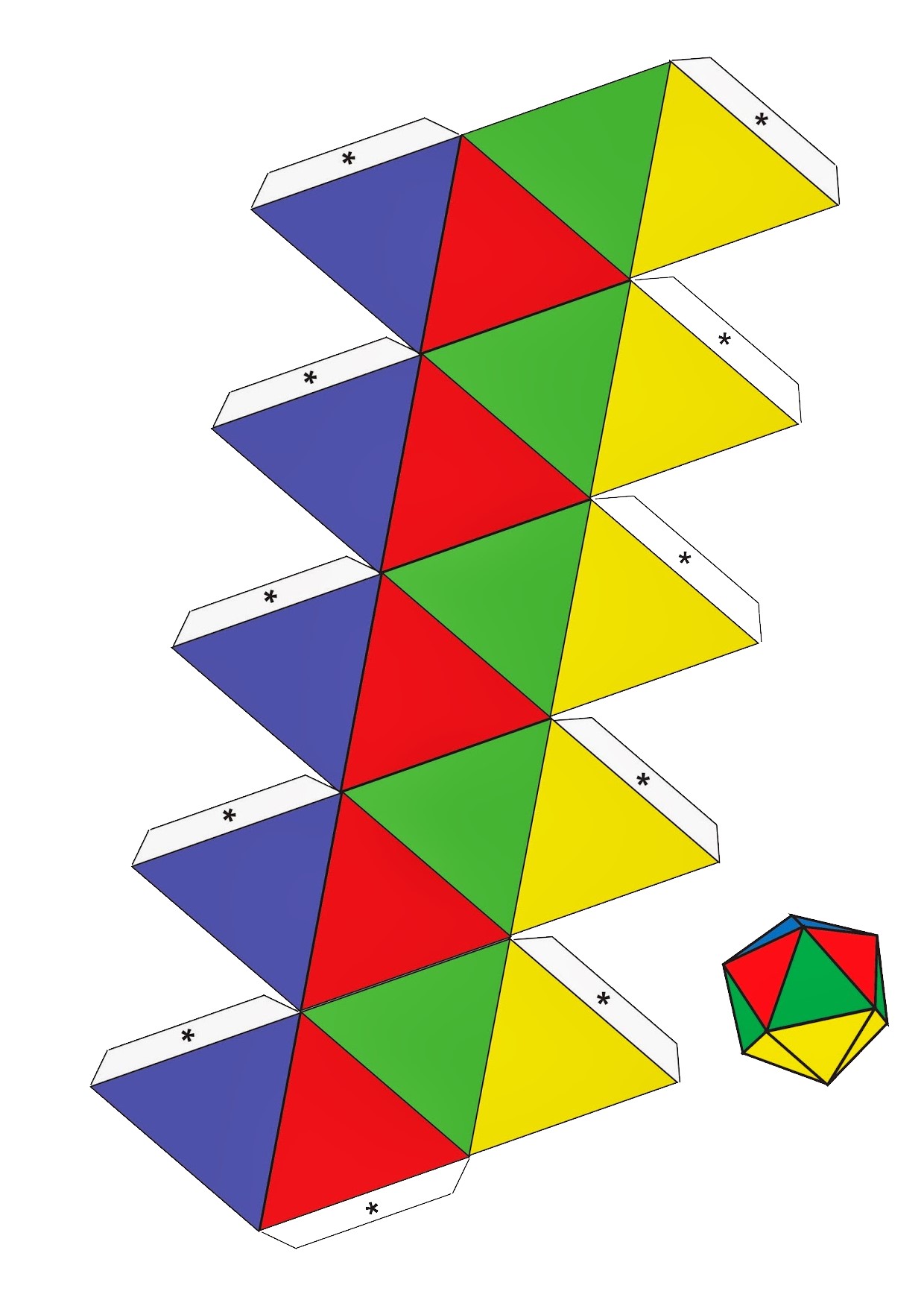







Эта страница содержит список правильных многомерных многогранников политопов и правильных cоединений этих многогранников в евклидовом , сферическом и гиперболическом пространствах разных размерностей. Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику n-1 -сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера , которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера [en].